The future of solar starts now
Discover what makes the Aurora platform the most accurate, profitable way to deliver every stage of the solar product lifecycle.
Discover what makes the Aurora platform the most accurate, profitable way to deliver every stage of the solar product lifecycle.

Create a highly accurate solar design without having to visit the site, saving time and money during the quoting process.
Learn More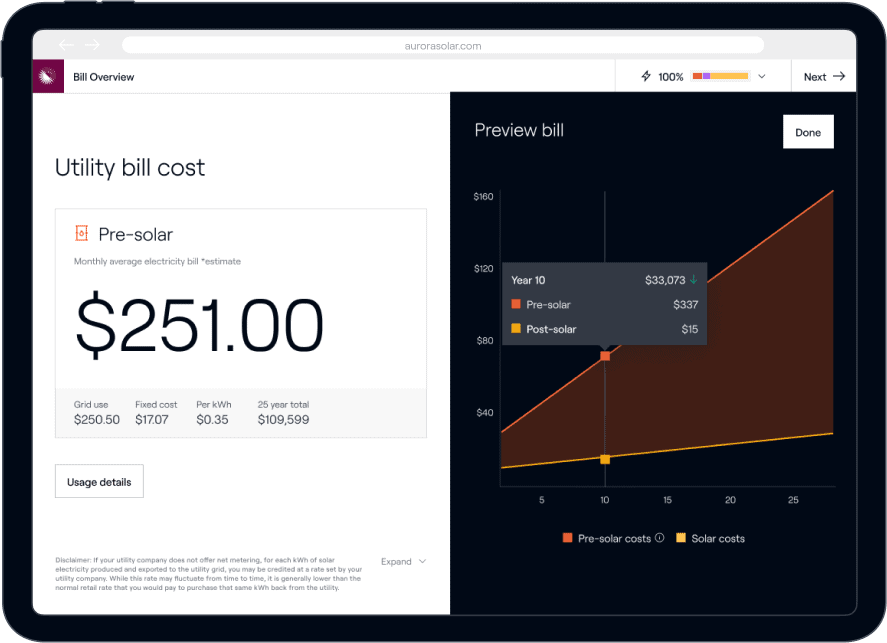
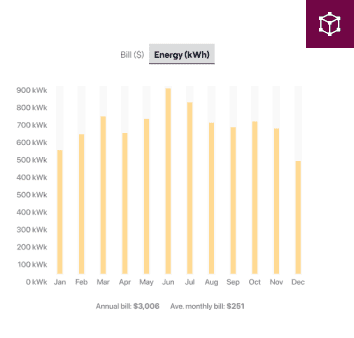
Create a proposal with personalized, permit-quality accuracy with just an address and an electric bill. Your customers get a premium experience and you save time.
Learn More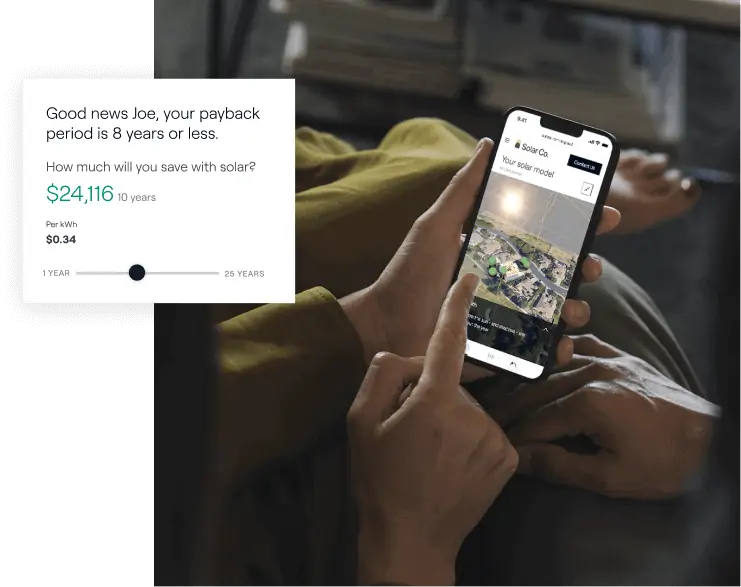

Engage homeowners with an instant, personalized 3D solar estimate that builds your brand credibility and makes you stand out from the rest.
Learn MoreWe’ve outclassed our competition so you can conquer yours
Leading solar companies depend on Aurora to outpace the industry. Here's proof:
I would go as far as to say it’s impossible to scale without a tool like Aurora. It makes sure we’re not pitching things we can’t uphold or making promises we can’t deliver on.
We found that [SolarGraf] wasn’t as technically oriented as our sale was. That’s when we decided to look at other softwares that would give our reps and clients the accuracy they need to make the right buying decision on solar… Aurora is the only tool in the market that matches the technical acumen of our team.
"It's all about customer expectations. It's a great experience for everyone: the rep, the company, the customer. It makes the whole process easier when you get it right from the start."
Learning how to use Sales Mode was almost immediate – everything is right where it needs to be. Sales Mode is probably the easiest aspect of my job.
Never once with Aurora have I been in a position where I’ve felt like I’ve over-promised and under-delivered.
Because it [Aurora] builds a house for you, it's super simple. You're basically adding the panels and getting the panel count right, and you're done. I could create a proposal in probably like less than three minutes. That’s how great it is.
More jobs are going to install because the homeowner feels confident that they’re actually going to get what we originally showed them.
We can see so many people so much faster. There was no way I could run 4-7 appointments per day using the tools we had before.
Interviews with installers using Aurora’s 3D modeling with shade and tilt analysis during the sales process found that its implementation resulted in as much as a 99 percent reduction in change orders.
Submitting the plan set was as smooth as can be and we had no issues with the AHJ. Our team has already saved a ton of time with this service.
The final product that we’re presenting to the homeowner is just so much more professional. The 3D models, sunpath, LIDAR, and other tools are very effective in a sale.
I would go as far as to say it’s impossible to scale without a tool like Aurora. It makes sure we’re not pitching things we can’t uphold or making promises we can’t deliver on.
We found that [SolarGraf] wasn’t as technically oriented as our sale was. That’s when we decided to look at other softwares that would give our reps and clients the accuracy they need to make the right buying decision on solar… Aurora is the only tool in the market that matches the technical acumen of our team.
"It's all about customer expectations. It's a great experience for everyone: the rep, the company, the customer. It makes the whole process easier when you get it right from the start."
Learning how to use Sales Mode was almost immediate – everything is right where it needs to be. Sales Mode is probably the easiest aspect of my job.
Never once with Aurora have I been in a position where I’ve felt like I’ve over-promised and under-delivered.
Because it [Aurora] builds a house for you, it's super simple. You're basically adding the panels and getting the panel count right, and you're done. I could create a proposal in probably like less than three minutes. That’s how great it is.
More jobs are going to install because the homeowner feels confident that they’re actually going to get what we originally showed them.
We can see so many people so much faster. There was no way I could run 4-7 appointments per day using the tools we had before.
Interviews with installers using Aurora’s 3D modeling with shade and tilt analysis during the sales process found that its implementation resulted in as much as a 99 percent reduction in change orders.
Submitting the plan set was as smooth as can be and we had no issues with the AHJ. Our team has already saved a ton of time with this service.
The final product that we’re presenting to the homeowner is just so much more professional. The 3D models, sunpath, LIDAR, and other tools are very effective in a sale.
When you’re selling as much as we’re selling, you have to be able to deliver build-ready projects to your operations team. When sales and operations are aligned, that ultimately allows us to sell more. Aurora has allowed us to bridge that gap.
Most other tools out there are just proposal skins that give rough estimates – and we've used them all. We were so impressed with Aurora's technology that we decided to use them for everything, all the way from proposal to the design, because accuracy is so important.
When we can be accurate on the front-end it helps reduce timelines on the back-end – and that cuts weeks and weeks out of projects.
We’ve had 4 cases where customers didn’t agree with the measurements on the Aurora design that we presented virtually. We decided to go out to the site and measure the house by hand with the homeowner, and in every instance, Aurora was correct. They were actually wrong about the measurements of their own home. The accuracy of the Aurora software, combined with our willingness to put it to the test on-site, helped close the deal each time!
It's such a game-changer that we don’t have to take Suneye readings anymore which saves us time and money. It's wonderful to utilize a platform like Aurora to be so confident in what the system will produce.
Aurora has given us the ability to design efficiently and be confident that we’re providing to the customer a detailed representation of what is going to be on-site without traveling there.
In less than a month utilizing Aurora’s Lead Capture AI, we were able to quadruple our web lead volume, and we see 25% higher set rates from our organic leads compared to those generated through other marketing channels. In my estimation, Lead Capture AI is effective because the tool leverages engaging visuals with readily quantified benefits, helping potential clients understand not only their savings, but what solar would realistically look like on their home.
Previous software was a very manual process, so sales reps could spend 2 hours in the home. Now they can get all of that done in about 20 mins.
We can now create a design for a home in a predetermined amount of time. When it becomes more of a push-of-a-button as opposed to an order, it definitely helps our efficiency. When that pipeline of jobs becomes exponentially bigger, it becomes more and more critical.
The value add to the sales process was huge because we can actually walk through the design with the homeowner. The customer feels like we’re redesigning and building it with them which lends more credibility to us as a company and makes it seem like we’re not just salespeople.
It's all about customer expectations. It's a great experience for everyone: the rep, the company, the customer. It makes the whole process easier when you get it right from the start
When you’re selling as much as we’re selling, you have to be able to deliver build-ready projects to your operations team. When sales and operations are aligned, that ultimately allows us to sell more. Aurora has allowed us to bridge that gap.
Most other tools out there are just proposal skins that give rough estimates – and we've used them all. We were so impressed with Aurora's technology that we decided to use them for everything, all the way from proposal to the design, because accuracy is so important.
When we can be accurate on the front-end it helps reduce timelines on the back-end – and that cuts weeks and weeks out of projects.
We’ve had 4 cases where customers didn’t agree with the measurements on the Aurora design that we presented virtually. We decided to go out to the site and measure the house by hand with the homeowner, and in every instance, Aurora was correct. They were actually wrong about the measurements of their own home. The accuracy of the Aurora software, combined with our willingness to put it to the test on-site, helped close the deal each time!
It's such a game-changer that we don’t have to take Suneye readings anymore which saves us time and money. It's wonderful to utilize a platform like Aurora to be so confident in what the system will produce.
Aurora has given us the ability to design efficiently and be confident that we’re providing to the customer a detailed representation of what is going to be on-site without traveling there.
In less than a month utilizing Aurora’s Lead Capture AI, we were able to quadruple our web lead volume, and we see 25% higher set rates from our organic leads compared to those generated through other marketing channels. In my estimation, Lead Capture AI is effective because the tool leverages engaging visuals with readily quantified benefits, helping potential clients understand not only their savings, but what solar would realistically look like on their home.
Previous software was a very manual process, so sales reps could spend 2 hours in the home. Now they can get all of that done in about 20 mins.
We can now create a design for a home in a predetermined amount of time. When it becomes more of a push-of-a-button as opposed to an order, it definitely helps our efficiency. When that pipeline of jobs becomes exponentially bigger, it becomes more and more critical.
The value add to the sales process was huge because we can actually walk through the design with the homeowner. The customer feels like we’re redesigning and building it with them which lends more credibility to us as a company and makes it seem like we’re not just salespeople.
It's all about customer expectations. It's a great experience for everyone: the rep, the company, the customer. It makes the whole process easier when you get it right from the start